Sonlu Elemanlar Yöntemi (FEM) ve Mesh Teknikleri
Sonlu Elemanlar Yöntemi (FEM), 1950’lerin sonlarından bu yana mühendislik problemlerini çözmek için güçlü bir araç olarak kullanılmıştır. Başlangıçta hesaplamalar elle yapılmaktaydı ve yöntem, günümüzde kullanılan yer değiştirme tabanlı yaklaşım yerine kuvvet tabanlıydı. Bilgisayar teknolojisindeki ilerlemelerle birlikte, çeşitli ticari FE yazılımları ortaya çıkmış ve FEM’in yetenekleri ve verimliliği büyük ölçüde artmıştır.
FEM’de Eleman Türlerinin Önemi
FEM’in doğru sonuçlar üretebilmesi için yeterli sayıda eleman kullanılması büyük önem taşır. Çözüm sürelerini kısaltmak ve daha az bilgisayar gücü gerektirdiğinden, gerekli şartlar sağlanıyorsa katı (solid) elemanlar, kabuk (shell) veya kiriş (beam) elemanlara dönüştürülebilir. Kabuk ve kiriş elemanlar, özellikle ince yapılar ve uzun elemanlar için hesaplamaları hızlandırarak modelleme sürecini daha verimli hale getirir.
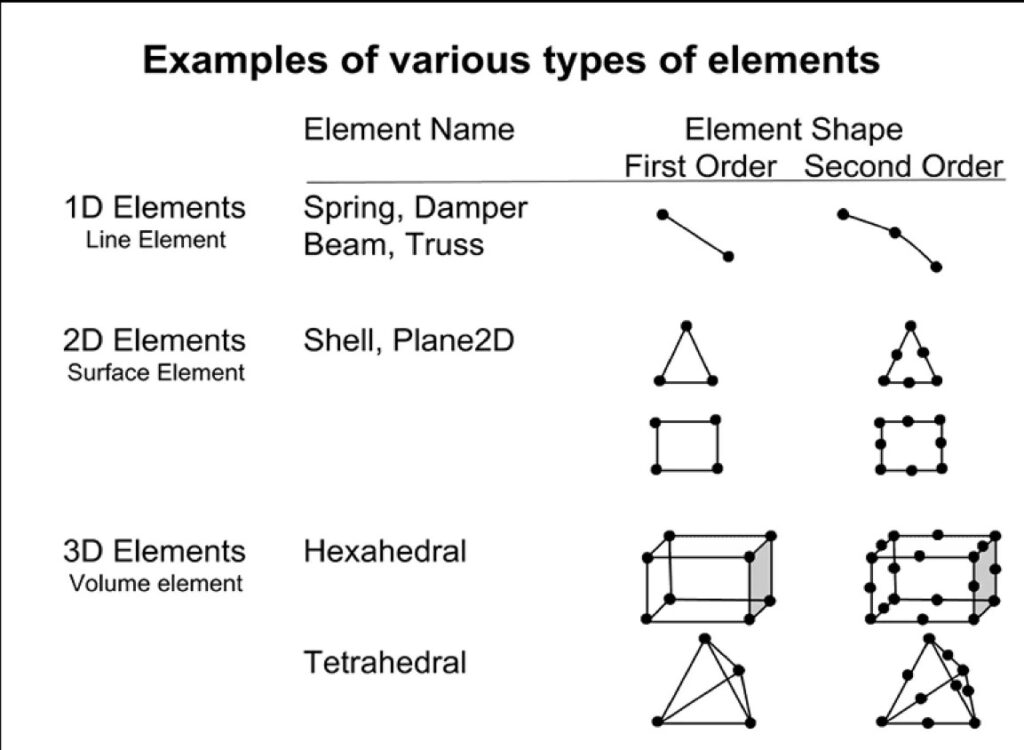
Belirli eleman türlerini kullanmak, çözüm süresini önemli ölçüde azaltabilir. Örneğin, basit bir yükleme durumunuz varsa ve sadece yüzeydeki gerilmeyi incelemek istiyorsanız, çok ayrıntılı bir mesh veya karmaşık bir eleman türü kullanmanıza gerek olmayabilir. Modeli olabildiğince basitleştirmek her zaman daha iyidir.
Eleman Sınıflandırması
2D’de elemanlar, şekillerine göre genellikle üçgen veya dörtgen olarak sınıflandırılır. Ayrıca, sahip oldukları düğüm sayısına göre de değişebilirler:
- TRI3: 3 düğümlü üçgen
- TRI6: 6 düğümlü üçgen
- QUAD4: 4 düğümlü dörtgen
- QUAD8: 8 düğümlü dörtgen
Genel olarak, daha fazla düğüme sahip elemanlar, daha yüksek bir deformasyon temsili doğruluğu sağlar.
3D elemanlar için, temel olarak 2D elemanların 3D versiyonlarıdır ve genellikle tetrahedral ve hexahedral elemanlar olarak adlandırılırlar. Bu elemanlar da düğüm sayısına göre değişebilir:
- TET4: 4 düğümlü tetrahedron
- TET10: 10 düğümlü tetrahedron
- HEX8: 8 düğümlü hexahedron
- HEX20: 20 düğümlü hexahedron
Aşağıdaki şekilde derecelerine göre eleman tipleri gösterilmektedir.
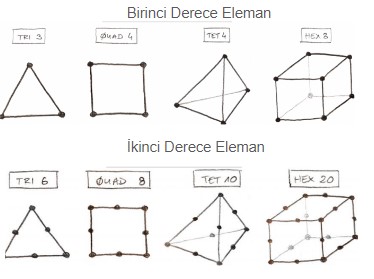
Mesh Yöntemleri
Çeşitli mesh yöntemleri, mesh yapılarını oluşturmak için kullanılır ve her biri kendi güçlü yönlerine ve ideal uygulama alanlarına sahiptir:
Tetrahedrons (Dört Yüzlüler)
Bu yöntem, üçgen elemanlar kullanarak mesh oluşturur. Özellikle girintili çıkıntılı geometriler, kanallar ve açılı köşeler gibi karmaşık geometriler için uygundur. Tetrahedral meshler, aynı mesh boyutuna sahip dörtgen elemanlardan daha fazla hücre içerebilir.
Hex Dominant (Altıgen Baskın)
Altıgen baskın meshleme, çoğunlukla hexahedral elemanlardan oluşan meshler oluşturmayı amaçlar. Bu yöntem, başlangıç meshindeki üçgenleri dörtgenlere dönüştürmek için üçgen birleştirme tekniğini kullanır. Bu nedenle, tüm elemanlarınızın hexahedral olacağı anlamına gelmez. Mesh geometrisinde yine birçok üçgen veya prizmatik eleman göreceksiniz.
Sweep (Süpürme)
Süpürülmüş mesh yöntemi, bir yüzeyin yüksek kaliteli dörtgen elemanlarla meshlenmesi ve ardından bu elemanların hacim boyunca “süpürülmesi” ile oluşturulur. Bu yöntem, hacim boyunca sabit bir kesite sahip cisimler için uygundur.
Multizone (Çok Bölgeli)
Multizone yöntemi, geleneksel süpürme yaklaşımı için çok karmaşık olan tek parçalı cisimleri meshlemek için kullanılır. Multizone mesh yöntemi, geometrinin otomatik olarak yapılandırılmış (süpürülebilir) ve serbest (yapılandırılmamış) bölgelere ayrılmasını sağlar. Mümkün olan yerlerde saf hexahedral meshler oluşturur ve daha zor yakalanan bölgeleri yapılandırılmamış mesh ile doldurur.
Cartesian (Dikdörtgen)
Dikdörtgen hücre yaklaşımı, optimizasyon gerektirmeden mesh oluşturur, böylece simülasyon sürecindeki önemli bir darboğazı ortadan kaldırır. Ancak, sınırda oluşturulan küçük hücreler, simülasyon için zaman adımı üzerinde ciddi kısıtlamalar getirebilir. Bu küçük hücre problemini, düzenli hücre zaman adımını kullanarak çözümleri geliştirerek ve kararlılığı koruyarak aşmak gereklidir.
Aşağıdaki şekilde mesh yöntemleri gösterilmektedir.

Mesh Kalitesi Değerlendirme Kriterleri
Sonlu elemanlar yöntemi için yapılandırılmamış başlangıç meshlerinin otomatik olarak oluşturulmasında mesh kalite metriklerinin kullanımı esastır. Bu metrikler olmadan, oluşturulan meshin hesaplama analizi yapmaya yetecek asgari kaliteye sahip olup olmadığını belirlemek zordur. Bu durum, özellikle hexahedral meshlerin otomatik oluşturulmasında geçerlidir çünkü hexahedral mesh oluşturma algoritmalarının çok azı asgari mesh kalitesi garantisi sağlar.
Mesh hücresinin “kalitesi” birkaç şekilde ölçülebilir. Mesh elemanlarının kalitesini belirlemek için çeşitli geometrik kontroller yapılır. Bu kontrol metrikleri şunlardır:
- Eleman Kalitesi
- Üçgenler için En-Boy Oranı Hesaplaması
- Dörtgenler için En-Boy Oranı Hesaplaması
- Jacobian Oranı
- Bükülme Faktörü
- Paralel Sapma
- Maksimum Köşe Açısı
- Eğrilik
- Ortogonal Kalite
Eleman Kalitesi
Eleman Kalitesi, 2D dörtgen/üçgen elemanlar için hacmin, kenar uzunluklarının karelerinin toplamına oranına, veya 3D elemanlar için kenar uzunluklarının karelerinin toplamının küp köküne oranına dayanır. Değeri 1 olan bir eleman mükemmel bir küp veya kareyi, 0 olan bir eleman ise sıfır veya negatif hacmi temsil eder. Sonlu elemanlar yöntemi, biyomekanik ve medikal uygulamalar ve inşaat mühendisliği uygulamalarında dikkate alınır.
En-Boy Oranı (Aspect Ratio)
Üçgenin en-boy oranı, üçgenin “yüksekliği” ve “genişliği”nin karşılaştırmasını sağlar. 1’den sonsuza kadar değişir. 1.0 değeri eşkenar üçgeni gösterir. Aşağıdaki görsel, 1 ve 20 en-boy oranlarına sahip üçgenleri gösterir. Dörtgenlerin en-boy oranı, uzun kenarın kısa kenara oranını verir. 1.0 değeri bir kareyi gösterir. Aşağıdaki görsel, 1 ve 20 en-boy oranlarına sahip dörtgenleri gösterir. Elektromanyetik alan analizleri ve sonlu elemanlar yöntemi uygulamalarında dikkate alınır.
Jacobian Oranı
Jacobian oranı, verilen bir elemanın şeklinin ideal bir elemanın şekline kıyasla ölçüsüdür. Eleman türüne bağlı olarak ideal şekil değişir. İdeal Jacobian oranı 1.0’dır ve iyi bir kaliteye sahip mesh, elemanlarının %90’ından fazlasının Jacobian oranının 1 ile 10 arasında olmasını sağlar. Sonlu elemanlar yöntemi ve biyomekanik ve medikal uygulamaların olduğu analizlerde dikkate alınır.
Bükülme Faktörü (Warping Factor)
Bükülme faktörü bazı dörtgen kabuk elemanları ve tuğla, kama ve piramitlerin dörtgen yüzleri için hesaplanır ve test edilir. İdeal bükülme faktörü 0’dır. Bükülme, bükülme ve bozulmanın bir ölçüsüdür ve en iyi şekilde farklı bükülme faktörlerine sahip dörtgenlere bakarak anlaşılır. Akışkanlar dinamiği ve jeomekanik ve yer bilimleri gibi uygulama alanlarında dikkat edilir.
Paralel Sapma (Parallel Deviation)
Paralel sapma, bir şeklin iki paralel kenarının ne kadar saptığını ölçer. Kare için ideal paralel sapma 0’dır. Akışkanlar dinamiği ve jeomekanik ve yer bilimleri gibi uygulama alanlarında dikkat edilir.
Maksimum Köşe Açısı
Bu, bir elemanın bitişik kenarları arasındaki maksimum açıdır. Üçgen için en iyi maksimum açı 60 derecedir. Dörtgen için ise 90 derecedir. Elektromanyetik alan analizleri ve inşaat mühendisliği uygulamalarında dikkat edilir.
Eğrilik (Skewness)
Eğrilik, bir meshin birincil kalite ölçütlerinden biridir. Eğrilik, bir yüzeyin veya hücrenin ideal (eşkenar veya eş açılı) olup olmadığını belirler. Elektromanyetik alan analizleri ve jeomekanik ve yer bilimleri uygulama alanlarında dikkat edilir.
Ortogonal Kalite (Orthogonal Quality)
Bu, iki mesh düğümünü (veya kontrol hacmini) bağlayan vektör ile bu kenarla ilişkili her yüzey entegrasyon noktası (n) için normal vektör arasındaki açıyı içerir. Ortogonal kalite aralığı 0-1’dir; burada 0 en kötü ve 1 en iyidir. Akışkanlar Dinamiği ve biyomekanik ve medikal uygulamaların olduğu analizlerde dikkat edilir.
Aşağıdaki şekilde mesh kalitesi renk sıkalası gösterilmektedir.
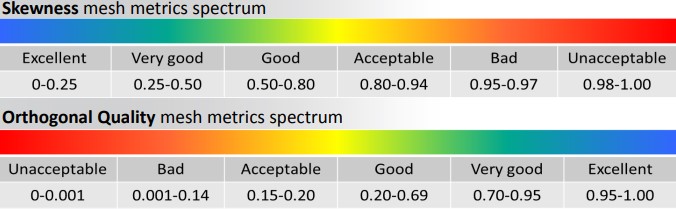

 tr
tr