HESAPLAMALI AKIŞKANLAR DİNAMİĞİ (HAD) NEDİR?
Günümüz mühendisliğinin temel taşlarından biri olan Hesaplamalı Akışkanlar Dinamiği-HAD (Computational Fluid Dynamics-CFD) nedir ve neden bu kadar önemlidir?
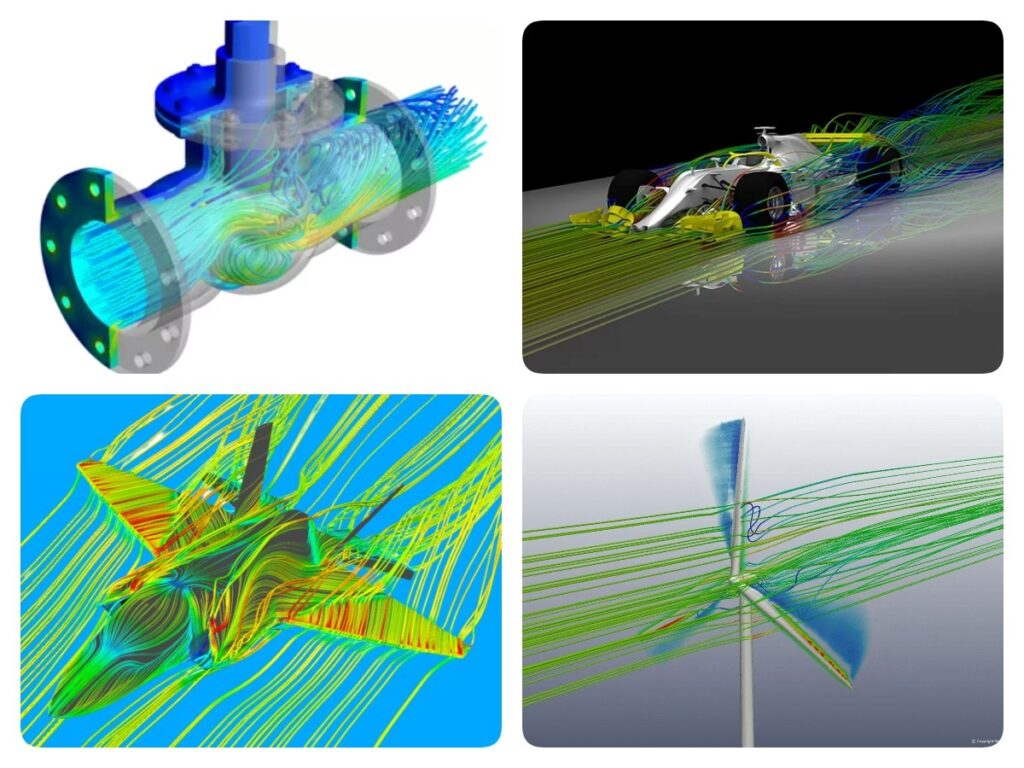
HAD, akışkanların hareketini sayısal yöntemlerle modelleme ve analiz etme sürecini ifade eder. Mühendislik hesaplamalarında, akışkan hareketinin doğru tespit edilmesi oldukça önemlidir. Akışkan hareketi genel bağlamda deneysel, teorik ve hesaplamalı (nümerik) olmak üzere üç yoldan biriyle incelenir. Analitik yöntemlerle direkt olarak hesaplanamayan kompleks modellerde ısı transferi, basınç kayıpları, akış hızları gibi verilerin nümerik yöntemlerle parçanın tasarım aşamasındayken belirlenmesi, zaman ve maliyet açısından önemli avantajlar sağlamaktadır. Bu verilerin klasik akışkanlar mekaniğinin temel denklemleriyle çözümlenmesi ise çok zor hatta çoğunlukla imkansızdır. Gelelim Hesaplamalı Akışkanlar Dinamiği’nin tanımına:
Hesaplamalı Akışkanlar Dinamiği Nedir?
HAD (Hesaplamalı Akışkanlar Dinamiği), temel olarak akışkan davranışının etkili olduğu problemlerin, sayısal metot ve algoritmalar ile bilgisayar üzerinde çözülerek analiz edildiği, akışkanlar mekaniğinin bir koludur. Çok fazlı akışlar, newtonian veya newtonian olmayan akışlar, katı-sıvı etkileşim analizleri, ileri türbülans modelleri, dönen parçaların analizleri gibi birçok uygulamada HAD, doğru ve hızlı sonuç elde etmemizi sağlar. Örnek vermek istersek havanın uçağın kanatları üzerindeki akışını, yağın borular içindeki hareketini veya suyun gemi gövdesi etrafındaki davranışını anlamamız için bir yöntemdir. Sonuca ulaşmak için akış bölgesi, akışa ait temel diferansiyel denklemleri simüle eden küçük düzgün elemanlardan ve noktalardan oluşmuş ağ yapısına ayrılır ve bu küçük elemanlardan iterasyonlarla adım adım bütün çözüme varılır.
Hesaplamalı Akışkanlar Dinamiğinin Getirileri Nelerdir?
- HAD, deneysel akışkan dinamiğine göre daha maliyet-etkindir ve daha hızlı sonuç verir.
- HAD, deney yapılmasının güç ya da imkânsız olduğu fiziksel olayların modellenmesine imkân sağlar.
- Gözlenen akış bölgesi içinde deneysele kıyasla daha ayrıntılı incelenebilir ve değerlendirilebilir veriler sunar. Deney esnasında ölçülemeyen, gözlemlenemeyen pek çok veriye hesaplamalı akışkanlar dinamiği ile ulaşılabilir.
- Tehlikeli olayların (patlamalar, radyasyon, kirlenme gibi) bulunduğu senaryoların incelenmesine olanak tanır.
- Tam ölçek benzetimler sağlayabilir. Örneğin gerçek denizaltı üzerindeki, çeşitli kule konumlarının, pervanenin akustik nitelikleri üzerindeki etkisinin incelenmesi gerekli olsa bu verilere deney yoluyla ulaşmak hemen hemen imkânsız olurdu veya öngörülen bir kasırganın gemi üst yapısı üzerindeki etkisi incelenmek istendiğinde HAD kullanılmaksızın bu yapılamazdı.
HAD Uygulamasının Aşamaları
Bir HAD uygulaması, üç temel aşamadan meydana gelir: ‘’ön işlem, çözüm, son işlem.’’ Bu üç aşama sonunda elde edilen veriler, mevcut deney sonuçlarıyla karşılaştırılarak sonuçların yeterli hassasiyette olduğu doğrulanmaya çalışılır.
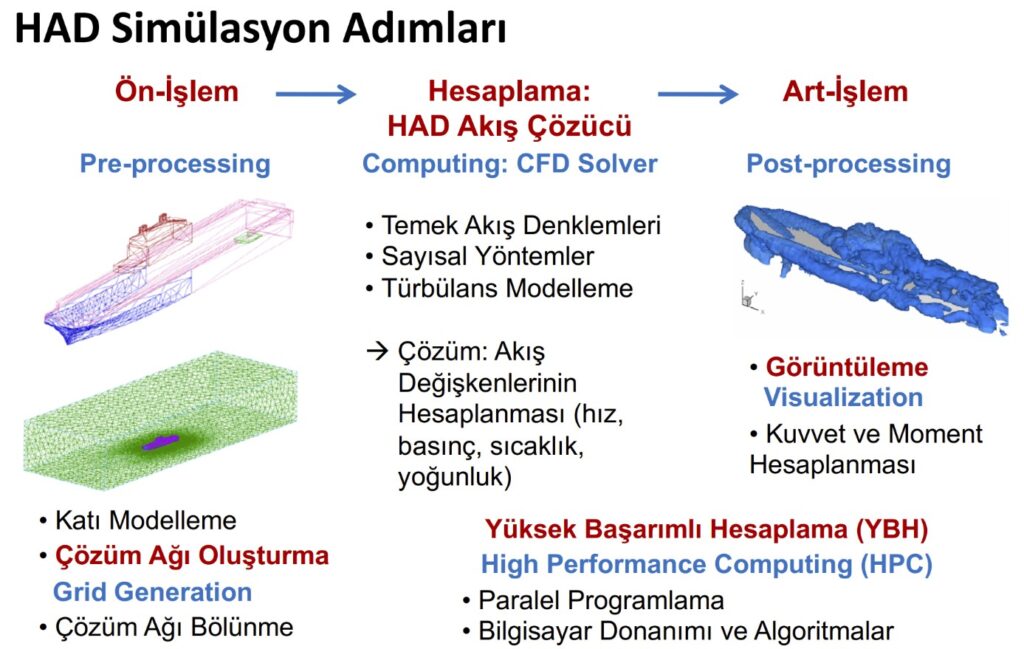
Ön İşlem: Model geometrinin oluşturulması, modelin ağ yapısının (mesh) oluşturulması, sınır şartlarının belirlenmesi aşamalarıdır. İncelenecek problemin çözüm aşamasına getirilmesi için yapılan bütün çalışmaları kapsar ve kullanılacak çözüm yöntemine uygun bir çalışmayı gerektirir. Geometri modelinin oluşturulmasını, problemin etki alanının belirlenmesi ve bu alanda (3 boyutlu uygulamalar için bu hacimde) ağ yapısının (mesh) oluşturulması takip eder. Oluşturulan sayısal modelin doğru çözülebilmesi için yapıya sınır şartları (Akışkanın giriş koşulları, simetri koşulları, fiziksel sınır koşulları, basınç koşulları, akışkanın çıkış koşulları…) tanımlanır.
Çözüm: Problemin türüne uygun bir çözüm yöntemiyle yaklaşık olarak hesaplanması basamağıdır. Çözüm aşamasında, sorunun biçimine bağlı olmak üzere analiz ve çözüm tipine göre hesaplama yapılır. Sayısal çözümleme de birkaç ara aşamadan oluşur. İlk aşama modelleme amacının belirlenmesidir. İkinci ara aşama sayısal çözüm modelinin tespit edilmesidir. Üçüncü ara aşamada fiziksel model seçimi tamamlanır. Son ara aşamada ise çözüm yöntemi seçimi yapılır.
Son işlem: Çözümde ulaşılan sonuçların değerlendirilmesidir. Sonuçlar genellikle grafiksel veya sayısal olarak değerlendirilir.
Hesaplamalı Akışkanlar Dinamiğinde Kullanılan Denklemler
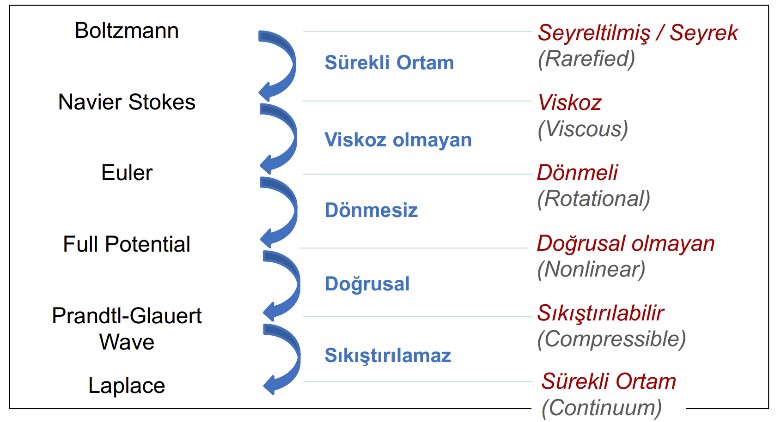
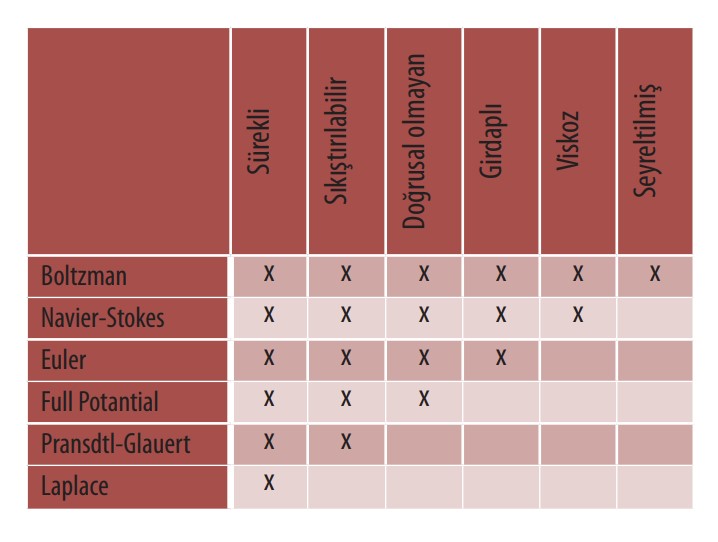

 tr
tr