Yapısal Analiz Uygulaması ile Kuş Çapma Analizi
Günümüz havacılık sektöründe hava araçlarının karşılaştığı en büyük risklerden birisi, kuş çarpmalarıdır. Bu durumun sonucunda maddi, hatta bazen de can kayıplı bir çok kaza meydana gelmektedir. Havacılık sektörünün gelişmesi ile, artan hızları ve azalan seslerinden dolayı hava araçlarının kuşlar tarafından fark edilme süreleri oldukça azalmaktadır.
Uçak ve kuş çarpmalarının büyük bir çoğunluğu havaalanlarının yakınlarında, hava araçlarının kalkışlarında ya da inişlerinde meydana gelmektedir. Bu çarpmalar genelde hava araçlarının kokpit, kanat ve jet motorlarının olduğu bölgelerde olmaktadır. Özellikle jet motorunun içine emilen kuş ya da kuşlar, motorun gövdesinin, türbin bıçaklarının ve çok sayıda bölgenin hasara uğramasına sebep olmaktadır.
Uçak ve kuş çarpmalarının büyük bir çoğunluğu havaalanlarının yakınlarında, hava araçlarının kalkışlarında ya da inişlerinde meydana gelmektedir. Bu çarpmalar genelde hava araçlarının kokpit, kanat ve jet motorlarının olduğu bölgelerde olmaktadır. Özellikle jet motorunun içine emilen kuş ya da kuşlar, motorun gövdesinin, türbin bıçaklarının ve çok sayıda bölgenin hasara uğramasına sebep olmaktadır.
Hava araçları üzerinde kuş çarpmasının etkilerini görmek için test ortamında incelenmesi maddi açıdan maliyetli olacağı için bu etkileri bilgisayar ortamında gerekli ileri düzey mühendislik yazılımlarından faydalanarak simülasyonlarının yapılması ve hesaplanması, maddi kayıpları minimum düzeyde tutacağı için büyük önem teşkil etmektedir.
Bu blog yazısında, kuş çarpması analizlerinin detaylarından bahsedilmiş olup, çözüm için farklı analiz yöntemlerinin kıyaslamaları yapılmıştır. Ayrıca, SIMULIAworks yazılımının Explicit çözücüsü kullanılarak SPH yöntemi ile kuş çarpması analizinin simülasyonları yapılmıştır.
Bu blog yazısında, kuş çarpması analizlerinin detaylarından bahsedilmiş olup, çözüm için farklı analiz yöntemlerinin kıyaslamaları yapılmıştır. Ayrıca, SIMULIAworks yazılımının Explicit çözücüsü kullanılarak SPH yöntemi ile kuş çarpması analizinin simülasyonları yapılmıştır.

Kuş Çarpması ve Modellemesi
Kuş çarpma analizlerinde kullanılan kuş geometri modelleri,
•Silindirik
•Elipsoid
•Küresel / Yarım Küresel
Analizlerde kullanılan kuş modellerinin malzeme özellikleri kuşların yapısı incelendiğinde, suyun malzeme özellikleri kuşun malzeme modellerine yakın olması sebebi ile genellikle kuşlar su olarak modellenmektedir.
•Silindirik
•Elipsoid
•Küresel / Yarım Küresel
Analizlerde kullanılan kuş modellerinin malzeme özellikleri kuşların yapısı incelendiğinde, suyun malzeme özellikleri kuşun malzeme modellerine yakın olması sebebi ile genellikle kuşlar su olarak modellenmektedir.

Analiz Yöntemleri
Kuş modelinin nümerik diskritizasyonu aşağıdaki yöntemler kullanılarak sağlanabilir;
•Lagrange
•Euler
•ALE
•SPH
•Lagrange
•Euler
•ALE
•SPH
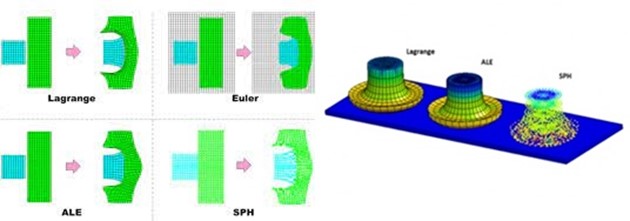
Lagrange Yöntemi
Lagrange modelleme yöntemi, sonlu elemanlar yazılımlarında standart olarak en çok kullanılan yöntemdir. Langrange yönteminde çözüm ağı üzerinde bulunan her bir düğüm noktası elaman üzerinde sabitlenmiş olarak bulunup, hareket esnasında ve deformasyon meydana geldiğinde eleman üzerinde bulunan malzeme düğüm noktaları ile birlikte sabit kalır.
Dezavantajı, çözüm ağı bozulmasıdır. Cisim üzerindeki büyük miktardaki şekil bozuklukları gerçekdışı sonuçların alınmasına yol açtığı gibi analizin hata vermesine sebep olmaktadır. Ayrıca katı cismin aşırı biçimde şekil değiştirmesi sonucunda meydana gelen kopmalar sonucu malzeme erozyonu analiz zamanını aşırı derece arttırmaktadır.
Avantajı, Lagrange yöntemi, sayısal olarak formülasyonunda katı cisimlere yönelik formülasyonlar içermesi ile katı cisimlerin analizi için çok iyi bir sonlu elemanlar yöntemidir
Avantajı, Lagrange yöntemi, sayısal olarak formülasyonunda katı cisimlere yönelik formülasyonlar içermesi ile katı cisimlerin analizi için çok iyi bir sonlu elemanlar yöntemidir
Euler Yöntemi
Euler metodunda temel olarak çözüm ağı kontrol hacmini simgelemektedir. Lagrange metodundaki akışkan davranışı sergileyen cisimler üzerindeki çözüm ağı bozulması ve her bir hesaplama için gereken küçük hesap adımları sorunlarına alternatif olarak Euler metodu kullanılabilir. Euler metodunda çözüm ağı, uzay ortamında sabit olup, malzeme bu sabit çözüm ağlı uzay ortamından ilerleyerek geçer.
Dezavantajı, sınır şartlarının net olarak cismi kapsamaması ve malzeme davranışının takibinin, düğüm noktalarının eleman üzerine sabit olmaması sebebiyle zorlaşması olarak kabul edilirken
Avantajı, küçük hesap aralıkları ile ihtiyac duyulan sorunlarının çözülmesi, çözüm ağı bozulması olmaması ve yüksek şekil değiştirmelerden dolayı yazılımsal hataların önüne geçilmesi olarak sıralanabilir.
Avantajı, küçük hesap aralıkları ile ihtiyac duyulan sorunlarının çözülmesi, çözüm ağı bozulması olmaması ve yüksek şekil değiştirmelerden dolayı yazılımsal hataların önüne geçilmesi olarak sıralanabilir.
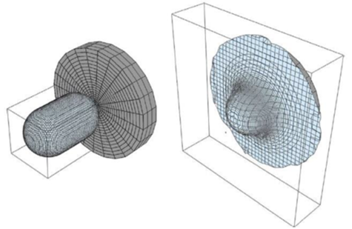
Rijid cisim analizlerinde Euler tekniği, Lagrange tekniğiyle karşılaştırıldığında her bir eleman başına çok daha fazla hesaplama gerektirdiği ve aynı sonuç için çok daha detaylı çözüm ağı gerektirdiği için daha fazla zamana ve hesaplama gücüne ihtiyaç duymaktadır.
Bu sebeple kuş çarpması analizinde hem akışkan hem de rijid cisim analizinin yapıldığı düşünüldüğünde bu yöntem verimli değildir.
Bu sebeple kuş çarpması analizinde hem akışkan hem de rijid cisim analizinin yapıldığı düşünüldüğünde bu yöntem verimli değildir.

ALE (Arbitrary Lagrangian-Eularian) Yöntemi
Euler yaklaşımında çözüm ağı uzayda sabit bir bölgeyi yansıtmaktadır, hesaplamanın yapılacağı bölge sadece malzemenin bulunduğu ortamın haricinde malzemenin muhtemel bulunacağı bölgeyi de kapsamalıdır. Bu nedenle Euler yaklaşımı, Lagrange yaklaşımına göre daha fazla hesaplamana gücü gerektirmektedir. Ayrıca Lagrange yaklaşımıyla aynı sonuca yaklaşabilmek için daha küçük yapıda çözüm ağı elemanlarına ihtiyaç duyulmaktadır.
Euler yönteminin tüm bu dezavantajları göz önünde bulundurulduğunda ALE yöntemi çok daha verimli analizler yapmaya imkân tanır. Euler metodunda bulunan sabit çözüm ağı, ALE (Arbitrary Lagrangian-Eulerian) yönteminde gerekli görüldüğü durumlarda hareket edebilir veya genişletilebilir. Kuş elemanının uzayda bulunduğu konuma uygun olarak ALE yaklaşımındaki çözüm ağı konumu güncellenir.
ALE ile daha az çözüm ağı elemanı gerekirken, hesaplama zamanları ciddi şekilde azalır. Ayrıyetten, rijid plak üzerinde çözüm ağı elamanları analiz sonucunda istenen doğruluğuna göre belirlenmelidir, dolayısıyla parçalanan kuş modelinin çözüm ağı elemanları çok önemlidir.
ALE ile daha az çözüm ağı elemanı gerekirken, hesaplama zamanları ciddi şekilde azalır. Ayrıyetten, rijid plak üzerinde çözüm ağı elamanları analiz sonucunda istenen doğruluğuna göre belirlenmelidir, dolayısıyla parçalanan kuş modelinin çözüm ağı elemanları çok önemlidir.

Genel olarak bakıldığında ALE yöntemi; Euler ve Lagrange yöntemlerinin iyi yönlerini bünyesine alarak daha verimli bir biçimde akışkan-katı cisim analizleri yapmaya imkân sağlamaktadır.
Diğer yandan Euler ve Lagrange yöntemlerinin dezavantajlarından da kurtulmaya çalışılmaktadır. ALE yönteminin kötü yanı kullanıcının çözüm ağı hacmini belirlerken deneyime sahip olmasını gerektirmesidir.
Diğer yandan Euler ve Lagrange yöntemlerinin dezavantajlarından da kurtulmaya çalışılmaktadır. ALE yönteminin kötü yanı kullanıcının çözüm ağı hacmini belirlerken deneyime sahip olmasını gerektirmesidir.
SPH Yöntemi
Lagrange, Euler ve ALE gibi yöntemlerin yanı sıra; çözüm ağı sorunlarından kurtulmak ve daha verimli analizler yapabilmek için çözüm ağsız SPH (Smoothed Particules Hydrodynamics) metodu geliştirilmiştir.
Büyük çapta deformasyonun meydana geldiği kuş çarpma problemi, SPH metodunun kullanımı için uygun olmasından dolayı, akışkan-katı cisim etkileşimli problemler, çarpışma simülasyonları, kırılgan ve eğilebilir yapıların analizleri ile yüksek deformasyona maruz kalınan analizler için kullanılmaktadır.

Yöntemlerin Kıyaslanması
Bu dört yöntem arasından Lagrange yöntemi genel olarak katı cisim analizlerinde kullanılmaktadır.
Euler yöntemi ise genellikle sıvı model analizlerinde kullanılmaktadır. Fakat kuş çarpması probleminde hem sıvı hem de katı elemanların bulunması, simülasyonun gerçeğe yakın sonuçlar vermesi açısından bu yöntemler yeterli gelmemektedir. Bu durumda incelenen diğer iki yöntem ALE ve SPH metotları daha uygulanabilir sonuçlar vermektedir.
Euler yöntemi ise genellikle sıvı model analizlerinde kullanılmaktadır. Fakat kuş çarpması probleminde hem sıvı hem de katı elemanların bulunması, simülasyonun gerçeğe yakın sonuçlar vermesi açısından bu yöntemler yeterli gelmemektedir. Bu durumda incelenen diğer iki yöntem ALE ve SPH metotları daha uygulanabilir sonuçlar vermektedir.

ALE yöntemi ise SPH metoduna göre yüksek hesaplama maliyetlerinin olması ve Euler kontrol hacmindeki ciddi şekil değişikliklerinin sonuçları etkilemesinden dolayı tercih edilmeyebilmektedir.
SPH yönteminde ise, kuş elemanında meydana gelen büyük miktardaki şekil bozulmaları en uygun şekilde temsil edilerek, gerçek şartlara uygun şekilde en yakın sonuçlara yakınsanmaktadır.
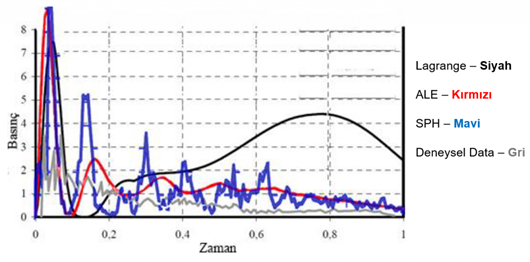
Aşağıda verilen grafikte farklı analiz yönteminden elde edilen basınç değişimlerinin sonuçları, deneysel datalar ile kıyaslanmıştır.
SPH yönteminde ise, kuş elemanında meydana gelen büyük miktardaki şekil bozulmaları en uygun şekilde temsil edilerek, gerçek şartlara uygun şekilde en yakın sonuçlara yakınsanmaktadır.
Aşağıda verilen grafikte farklı analiz yönteminden elde edilen basınç değişimlerinin sonuçları, deneysel datalar ile kıyaslanmıştır.
Kuş Çarpması Simülasyonu – SPH
Bu bölümde kuş çarpması analizi SIMULIAworks yazılımının Structural Mechanics Engineer rolü kullanılarak SPH yöntemi ile simülasyonu yapılmıştır. Bu simülasyon adımları aşağıda detaylandırılmıştır.
• Öncelikle Structural Mechanics Engineer rolü kullanılarak ‘Explicit’ çözücü içerisinde model tanımlaması yapılmalıdır.
• Hazırlanan model Explicit çözücüsü içerisinde transfer edilmelidir.
• Kuş geometrisi SPH modeli olarak tanımlanmalıdır.
• Analiz, Explicit çözücüsü ile çözdürülmelidir.
• Öncelikle Structural Mechanics Engineer rolü kullanılarak ‘Explicit’ çözücü içerisinde model tanımlaması yapılmalıdır.
• Hazırlanan model Explicit çözücüsü içerisinde transfer edilmelidir.
• Kuş geometrisi SPH modeli olarak tanımlanmalıdır.
• Analiz, Explicit çözücüsü ile çözdürülmelidir.

• Havacılık sektöründe, hava araçlarının (yoğunlukla uçakların) karşılaştığı büyük problemlerden biri olan kuş çarpması, maliyet ve hız düşünüldüğünde bilgisayar ortamında simülasyonlarının yapılması gerekmektedir.
• Bu simülasyonda çözüm yöntemlerinden en uygun olanı SPH (Smoothed Particules Hydrodynamics) yöntemidir.
• SPH yöntemi ile yapılan hesaplamalar yoğun oranda hafıza ve CPU işlem gereksinimi oluşturacağı için paralel çok işlemcili bilgisayarlar bu problemin önüne geçmektedir.
• Bu simülasyonda çözüm yöntemlerinden en uygun olanı SPH (Smoothed Particules Hydrodynamics) yöntemidir.
• SPH yöntemi ile yapılan hesaplamalar yoğun oranda hafıza ve CPU işlem gereksinimi oluşturacağı için paralel çok işlemcili bilgisayarlar bu problemin önüne geçmektedir.

Kaynaklar
• Wikipedia, http://en.wikipedia.org/wiki/Bird_strike
• Budgey, R. (2000). “The Development of a Substitute Artificial Bird by the International Birdstrike Research Group for Use in Aircraft Component Testing”. Birdstrike Avoidance Team, Central Laboratory, Sand Hutton.
• Do I., Day J., “Overview of ALE Method in LS-Dyna”, Lawrance Livermore Software Technology (LSTC), 2005
• V. K. Goyal, C. A. Huertas, T. J. Vasko, 2013. “Bird-Strike Modeling Based on the Lagrangian Formulation Using LS-DYNA”, Am. Trans. Eng. Appl. Sci. 2(2): 057-081.
• J. Lacome, “Smooth Particle Hydrodynamics (SPH): A New Feature in LS-DYNA”, in:Proceedings of the 6th International LS-DYNA Users Conference, 2000.
• J. Metrisin, B. Potter, “Simulating Bird Strike Damage in Jet Engines”, ANSYS Solutions 3 (4) (2001) 8–9.
• Donea, J., A. Huerta, J. Ponthot, and A. Rodríguez-Ferran (2004). “Arbitrary LagrangianEulerian Methods”. Encyclopedia of Computational Mechanics, Volume 1, Chapter 14.
• Hut, P., L. Hernquist, G. Lake, J. Makino, S. McMillan and T. Sterling (1997) “Smooth Particle Hydrodynamics: Models, Applications, and Enabling Technologies”, Proceedings form the Workshop Presented by the Institute for Advance Study at Princeton. June, 1997.
• Shultz, C. and J. Peters (2002). “Bird Strike Simulation Using ANSYS LS/DYNA”. Phoenix Analysis and Design Technologies, Inc.
• Iariajournals, http://www.iariajournals.org/systems_and_measurements
• SIMULIA, https://www.youtube.com/channel/UCHnSRUS2NWhDmDG1nb8qV_Q
• Budgey, R. (2000). “The Development of a Substitute Artificial Bird by the International Birdstrike Research Group for Use in Aircraft Component Testing”. Birdstrike Avoidance Team, Central Laboratory, Sand Hutton.
• Do I., Day J., “Overview of ALE Method in LS-Dyna”, Lawrance Livermore Software Technology (LSTC), 2005
• V. K. Goyal, C. A. Huertas, T. J. Vasko, 2013. “Bird-Strike Modeling Based on the Lagrangian Formulation Using LS-DYNA”, Am. Trans. Eng. Appl. Sci. 2(2): 057-081.
• J. Lacome, “Smooth Particle Hydrodynamics (SPH): A New Feature in LS-DYNA”, in:Proceedings of the 6th International LS-DYNA Users Conference, 2000.
• J. Metrisin, B. Potter, “Simulating Bird Strike Damage in Jet Engines”, ANSYS Solutions 3 (4) (2001) 8–9.
• Donea, J., A. Huerta, J. Ponthot, and A. Rodríguez-Ferran (2004). “Arbitrary LagrangianEulerian Methods”. Encyclopedia of Computational Mechanics, Volume 1, Chapter 14.
• Hut, P., L. Hernquist, G. Lake, J. Makino, S. McMillan and T. Sterling (1997) “Smooth Particle Hydrodynamics: Models, Applications, and Enabling Technologies”, Proceedings form the Workshop Presented by the Institute for Advance Study at Princeton. June, 1997.
• Shultz, C. and J. Peters (2002). “Bird Strike Simulation Using ANSYS LS/DYNA”. Phoenix Analysis and Design Technologies, Inc.
• Iariajournals, http://www.iariajournals.org/systems_and_measurements
• SIMULIA, https://www.youtube.com/channel/UCHnSRUS2NWhDmDG1nb8qV_Q

 tr
tr