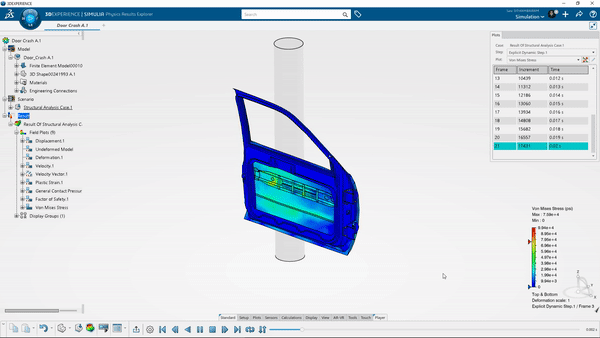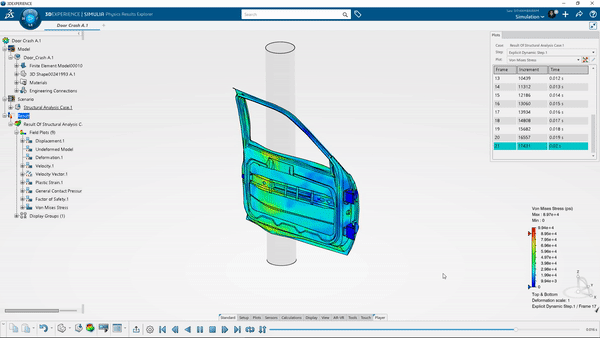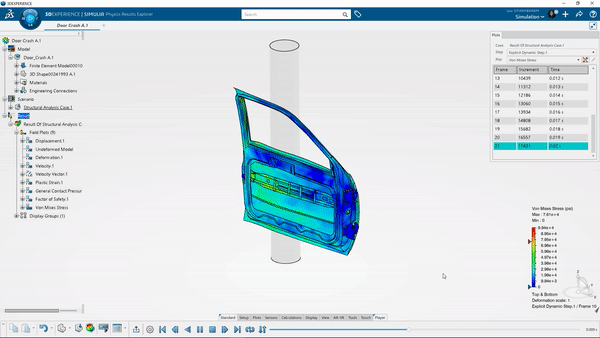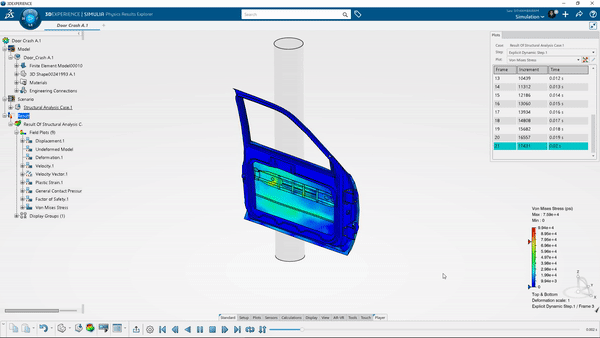
Implicit ve Explicit Yöntemi
Explicit ve implicit yöntemleri, fiziksel süreçlerin bilgisayar tabanlı simülasyonlarını gerektiren zamana bağlı olağan ve kısmi diferansiyel denklemlerin çözümlerine ulaşmak ve sayısal yaklaşımlar elde etmek için kullanılmaktadır. Bütün doğrusal olmayan ve dinamik analizler için sınır koşullarındaki uygulanan kuvvetlerin artımlı/kademeli olarak uygulanması gerekir. Bu sorunları çözmek için genellikle 'implicit' ve 'explicit' yöntemleri kullanılır.
Explicit yöntemleri sistemin anlık durumundan belli bir zaman sonraki durumunu hesaplarken, implicit yöntemleri hem sistemin mevcut durumunu hem de sonraki durumu içeren bir denklemi hesaplayarak çözüm bulunur.
Statik analizde, kütle (atalet) veya sönümleme etkisi yoktur. Dinamik analizde, kütle&atalet ve sönümleme ile ilişkili düğüm kuvvetleri dahil edilmiştir. Dinamik analiz, explicit veya implicit çözücü aracılığıyla yapılabilir.
Doğrusal olmayan implicit analizinde, her adımın çözümü belirli bir tolerans dahilinde denge kurmak için çözüm yinelemelerini gerektirir. Explicit analizinde düğüm ivmeleri doğrudan çözüldüğü için yineleme gerekmez.
Statik analizde, kütle (atalet) veya sönümleme etkisi yoktur. Dinamik analizde, kütle&atalet ve sönümleme ile ilişkili düğüm kuvvetleri dahil edilmiştir. Dinamik analiz, explicit veya implicit çözücü aracılığıyla yapılabilir.
Doğrusal olmayan implicit analizinde, her adımın çözümü belirli bir tolerans dahilinde denge kurmak için çözüm yinelemelerini gerektirir. Explicit analizinde düğüm ivmeleri doğrudan çözüldüğü için yineleme gerekmez.
Implicit ve Explicit Arasındaki Fark?
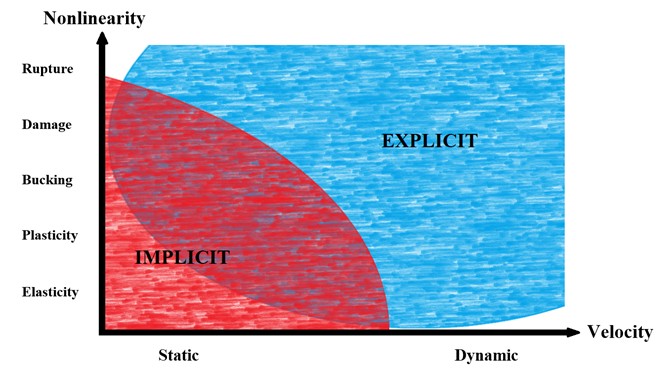
Implicit ve explicit analiz, zaman adımına (artışına) yaklaşımda ayrışır. İmplicit analizde, her zaman adımının yakınsaması gerekir ve zaman adımlarının süresi manuel olarak ayarlanabilir.
Implicit analizin tersine, explicit analizde her zaman adımının yakınsaması gerekmez, ancak çözümün doğruluğu için zaman adımları implicit analize kıyasla çok küçük olmalıdır.
Implicit analizin tersine, explicit analizde her zaman adımının yakınsaması gerekmez, ancak çözümün doğruluğu için zaman adımları implicit analize kıyasla çok küçük olmalıdır.
Implicit ve Explicit Hesaplamaları
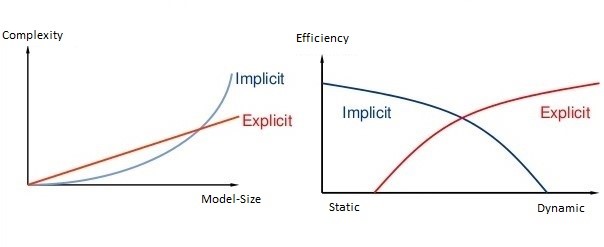
Implicit ve explicit hesaplamalar matematiksel kısmi diferansiyel denklemlerle ifade edilir. Bu matris denklemleri doğrusal veya doğrusal olmayan olabilir. Çoğu yapısal çalışmada, doğrusal olmayan denklemler üç kategoride değerlendirilir:
• Malzeme Nonlinearity:
• Geometrik Nonlinearity:
• Kontak Nonlinearity:
• Malzeme Nonlinearity:
• Geometrik Nonlinearity:
• Kontak Nonlinearity:
Fomülleştirme:
Doğrusal problemlerde, kısmi diferansiyel denklemleri matris denklemini şu şekilde basitleştirir:
[K]{x} = {f}
k = Sertlik matrisi
x = Yer değiştirme/sapma
F = Kuvvet
Doğrusal olmayan statik problemler için:
[K(x)]{x} = {f} → [k0 + k1• x + k2 • x2 +…]{x} = {f}
Dinamik problemler için matris denklemleri şöyle olur:
[M]{x´´} + [C]{x´} + [K]{x} = {f}
x´ = Hız
x´´ = İvme
C = Sönümleme matrisi
M = Kütle matrisi
[K]{x} = {f}
k = Sertlik matrisi
x = Yer değiştirme/sapma
F = Kuvvet
Doğrusal olmayan statik problemler için:
[K(x)]{x} = {f} → [k0 + k1• x + k2 • x2 +…]{x} = {f}
Dinamik problemler için matris denklemleri şöyle olur:
[M]{x´´} + [C]{x´} + [K]{x} = {f}
x´ = Hız
x´´ = İvme
C = Sönümleme matrisi
M = Kütle matrisi
Implicit Metod
Geometriye uygulanan yükler kademeli olarak yapıyı etkilediğinde ve gerinim oranı düşük olduğunda (saniyede 10^-3 'ten az) implicit method kullanılmalıdır. Gerinimin bir fonksiyonu olarak gerilme artışı belirlendiğinde, yapı implicit yöntemle analiz edilebilir.
Modeldeki genel denge, her zaman adımı için belirlenir. Bu durum, her zaman adımın yakınsaması gerektiği anlamına gelir.
Global denge yakınsadıktan sonra, çözücü her zaman adımı için tüm lokal sonlu eleman değişkenlerini (gerilmeler, gerinim, vb.) hesaplar.
• Avantaj: Genel denge her bir zaman adımında doğrulandığından ötürü bu zaman adımları büyük olabilir.
• Dezavantaj: Her zaman adımı yavaş hesaplanır ve genel dengeye ulaşmak için yinelemelere ihtiyaç vardır.
Modeldeki genel denge, her zaman adımı için belirlenir. Bu durum, her zaman adımın yakınsaması gerektiği anlamına gelir.
Global denge yakınsadıktan sonra, çözücü her zaman adımı için tüm lokal sonlu eleman değişkenlerini (gerilmeler, gerinim, vb.) hesaplar.
• Avantaj: Genel denge her bir zaman adımında doğrulandığından ötürü bu zaman adımları büyük olabilir.
• Dezavantaj: Her zaman adımı yavaş hesaplanır ve genel dengeye ulaşmak için yinelemelere ihtiyaç vardır.

Explicit Metod
Geometriye uygulanan yükler yapıyı aniden etkilediğinde ve gerinim oranı etkileri yüksek olduğunda saniyede 10^-3'e eşit veya daha fazla) explicit yöntemler kullanılmalıdır. Bu olaylar otomotiv kazası, balistik patlama, düşme vb. örneklerle açıklanabilir. Bu durumlarda, gerilmenin gerinim ile değişiminin yanı sıra, gerinim hızının da dikkate alınması gerekir.
Kontrol edilecek veya yinelenecek yakınsama kriteri yoktur. Çözücü doğrudan lokal sonlu eleman değişkenlerinin hesaplanmasına odaklanır.
Çözücü, hesaplanan zaman adımı için lokal sonlu eleman değişkenlerini hesaplar ve bir sonrakine geçer.
• Avantaj: Her zaman adımı son derece hızlı hesaplanır.
• Dezavantaj: Zaman adımı çok çok küçük olması gerekir. Aksi takdirde bu dengeyi sürdürmek imkansızdır.
Kontrol edilecek veya yinelenecek yakınsama kriteri yoktur. Çözücü doğrudan lokal sonlu eleman değişkenlerinin hesaplanmasına odaklanır.
Çözücü, hesaplanan zaman adımı için lokal sonlu eleman değişkenlerini hesaplar ve bir sonrakine geçer.
• Avantaj: Her zaman adımı son derece hızlı hesaplanır.
• Dezavantaj: Zaman adımı çok çok küçük olması gerekir. Aksi takdirde bu dengeyi sürdürmek imkansızdır.
Hangisi Daha İyi: Implicit veya Explicit?
Bu soru için kolay bir cevap mevcut değildir. Hem implicit hem de explicit çözücüler aynı tür problemleri çözer. Teknik olarak, her ikisi de tüm durumlar için aynı sonucu vermektedir. Aynı sorunu her iki yöntemle de analiz edebiliriz. İmplicit ve explicit arasındaki hayati fark, zaman artışı yaklaşımındadır.
• İmplicit analiz zaman adımının tanımlanmasına izin verir. Kullanıcılar, zaman adımının ne kadar büyük olması gerektiğini tanımlayabilir. Genel denge için bu zaman adımı iterasyonlarının tamamlanması gerekir. Bu nedenle, hesaplamak için biraz zaman gerektirir.
• Explicit analizde zaman adımları son derece hızlı hesaplanır çünkü, genel denge için iterasyon gerekli değildir. Ayrıca zaman adımı manuel olarak ayarlanamaz. Çözücü, kabul edilebilir bir zaman adımı olduğunu varsayar ve onunla birlikte hesaplar ki bu çok küçüktür.
• İmplicit analiz zaman adımının tanımlanmasına izin verir. Kullanıcılar, zaman adımının ne kadar büyük olması gerektiğini tanımlayabilir. Genel denge için bu zaman adımı iterasyonlarının tamamlanması gerekir. Bu nedenle, hesaplamak için biraz zaman gerektirir.
• Explicit analizde zaman adımları son derece hızlı hesaplanır çünkü, genel denge için iterasyon gerekli değildir. Ayrıca zaman adımı manuel olarak ayarlanamaz. Çözücü, kabul edilebilir bir zaman adımı olduğunu varsayar ve onunla birlikte hesaplar ki bu çok küçüktür.
Özetlersek
Analizdeki yükleme koşulları nispeten yavaş uygulanırsa, implicit çözücü gerçekten yararlıdır. İdeal analizler genellikle 1 saniyeden uzundur. Avantajı, zaman adımının (artışının) kullanıcıların istediği kadar büyük ayarlanabilmesidir.
1. Bilinmeyen x, sertlik matrisinin (K) çevrilmesiyle bulunur.
2. Newton-Raphson / Zorlanmış denge çözümleri.
3. Newton metodu kullanılır.
4. Daha hassas çözüm.
5. Büyük modeller için son derece zaman alıcı.
6. Daha fazla bilgisayar depolama alanı gerektirir.
7. Gerinim oranı saniyede 10^-3'ten az.
8. Yük oranlarının yavaş olduğu yapı dinamiği türleri için iyi bir karar;
• Yavaş uygulanan yer değiştirmeler
• Düşük frekans yanıtı
• Titreşim
• Salınım
1. Bilinmeyen x, sertlik matrisinin (K) çevrilmesiyle bulunur.
2. Newton-Raphson / Zorlanmış denge çözümleri.
3. Newton metodu kullanılır.
4. Daha hassas çözüm.
5. Büyük modeller için son derece zaman alıcı.
6. Daha fazla bilgisayar depolama alanı gerektirir.
7. Gerinim oranı saniyede 10^-3'ten az.
8. Yük oranlarının yavaş olduğu yapı dinamiği türleri için iyi bir karar;
• Yavaş uygulanan yer değiştirmeler
• Düşük frekans yanıtı
• Titreşim
• Salınım
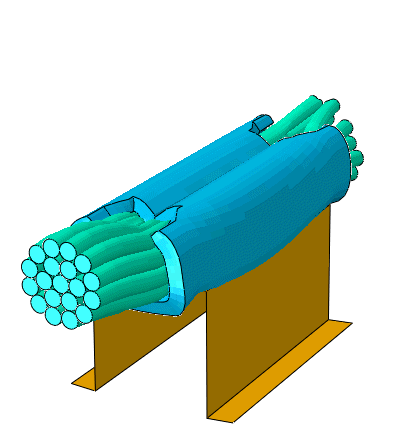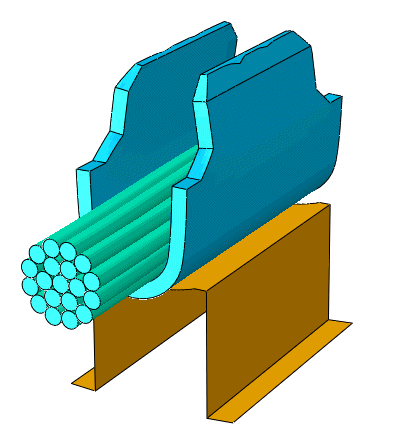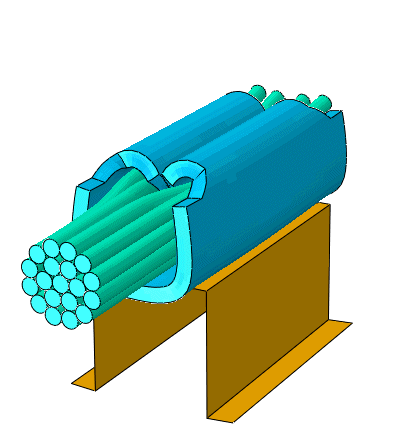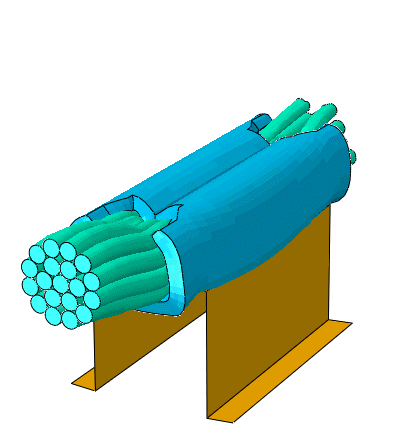
Explict çözücü, hızlı olaylar (çoğunlukla 0,1 saniyeden az) için mükemmeldir. Explicit çözücü, zaman adımın ne kadar büyük olması gerektiğini hesaplar ve zaman adımını ayarlar. Analizdeki zaman adımı, mesh (eleman boyutu ve eleman kalitesi), malzeme yoğunluğu ve young's modül değerlerine bağlıdır.
1. Bilinmeyen x, kütle matrisinin (M) çevrilmesiyle bulunur.
2. Doğrudan çözümler.
3. Merkezi fark yöntemleri kullanılır.
4. Daha düşük hassasiyet.
5. Kısa dinamik tepki süresine sahip büyük modellerin hesaplamasında verimli.
6. Daha az bilgisayar depolama alanı gerektirir.
7. Gerinim oranı saniyede 10^-3'e eşit veya daha fazla.
8. Dalga yayılımı olan yapı dinamiği türleri için iyi bir karar;
• Araba kazası
• Patlama etkisi
• Düşme testi
• Metal şekillendirme
1. Bilinmeyen x, kütle matrisinin (M) çevrilmesiyle bulunur.
2. Doğrudan çözümler.
3. Merkezi fark yöntemleri kullanılır.
4. Daha düşük hassasiyet.
5. Kısa dinamik tepki süresine sahip büyük modellerin hesaplamasında verimli.
6. Daha az bilgisayar depolama alanı gerektirir.
7. Gerinim oranı saniyede 10^-3'e eşit veya daha fazla.
8. Dalga yayılımı olan yapı dinamiği türleri için iyi bir karar;
• Araba kazası
• Patlama etkisi
• Düşme testi
• Metal şekillendirme
Kaynaklar
simscale.com
wikipedia.org
senterfea.com
fidelisfea.com
yasincapar.com
wikipedia.org
senterfea.com
fidelisfea.com
yasincapar.com

 tr
tr